 We have something a little different for the free Brick Math Lesson of the Month this time: a multi-day curriculum you can implement as a summer program or refresher course! "Building Skills with Brick Math" is the perfect way to help students strengthen their math skills within a limited time period. This one is for Basic Fractions, and there are programs for ten more math subjects that you can use with your students. To get your free Building Skills with Brick Math program for Basic Fractions, plus a new lesson each month, click here. If you'd like to see more Building Skills Summer Programs for other subjects, click here.  This curriculum is designed to be taught over 12 days. It includes a variety of learning techniques including manipulatives, drawing, verbal explanation, physical movement, and song. Students work with a partner, use the vocabulary fluently in math conversations, and assess themselves on their abilities. The teacher uses the lessons in the Teacher Edition, and the students follow along in their own Student Editions. At the end of the 12-day session, students will have sharpened their skills in Basic Fractions by following this innovative program.  Brick Math is a complete math curriculum for kindergarten through 8th grade that models the math with bricks. The curriculum is divided into 13 separate content areas: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, Decimals, Data and Statistics, and Pre-Algebra. Students can start anywhere in the curriculum. It can be used as a complete math curriculum or brought in as a supplement to help students who aren't having math success with other programs. Brick Math works in many applications: for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and affordable. For an innovative way to teach and learn K-8th grade math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves students' math test scores and hear what people who are using Brick Math have to say about the program.
0 Comments
 The FREE Brick Math Lesson of the Month for December 2023 is all about a tricky subject: Fraction Division. It comes from Fraction Division Using LEGO® Bricks and helps students understand a math subject area typically taught in grades 4-6. To get the December 2023 Brick Math Lesson of the Month, "Understanding Fraction Division," plus a new lesson each month, click here. Each Lesson of the Month includes the Teacher Lesson Guide as well as the Student Workbook Pages that correspond to the lesson.  The Lesson of the Month comes from Chapter 1 of Fraction Division. It's a great way to demonstrate the meaning of dividing fractions. Often students don't understand what dividing by a fraction really is, even if they can handle the mathematical algorithm of multiplying by the reciprocal. This lesson clearly shows the concept and relates it to division by whole numbers.  The lesson starts with a review of division by whole numbers, reminding students that "16 divided by 8" means breaking 16 into 8 groups , with 2 in each group. Then the lesson moves to an example with fractions, using the same terminology so students easily make the connection. The brick models help to demonstrate the concept. And this lesson includes two fraction division problems to help your students solidify the learning. Brick Math is a K-8 math curriculum that uses LEGO® bricks to model 13 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, Decimals, Data and Statistics, and Pre-Algebra.  Brick Math works in many applications: for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and affordable. If you are a math teacher or a parent with a student at home who is learning K-8th grade math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves students' math test scores and hear what people who are using Brick Math have to say about the program.  The Brick Math FREE Lesson of the Month for September 2023 is about Mixed Numbers and is taken from Basic Fractions Using LEGO® Bricks. The concept of a mixed number (a whole number and a fractional part) can be difficult for students to grasp, but modeling with bricks makes it so easy to learn. To get the September 2023 Brick Math Lesson of the Month, "Mixed Numbers," plus a new lesson each month, click here. Each Lesson of the Month includes the Teacher Lesson Guide as well as the Student Workbook Pages that correspond to the lesson. 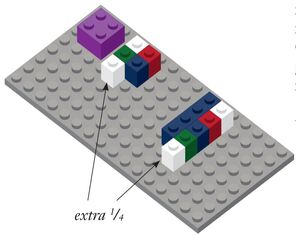 The lesson on mixed numbers first shows that a whole number can be divided into equal parts, and then shows how one more of that fractional part is added to the whole to make the mixed number. It's a very effective way to teach the concept of mixed numbers. It also shows the power of the Brick Math program, which makes math concepts visual and tactile so all students can learn them.  Brick Math is a K-8 math curriculum that uses LEGO® bricks to model 13 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, Decimals, Data and Statistics, and Pre-Algebra. Data and Statistics and Pre-Algebra expand the Brick Math curriculum to include grades 7 - 8. Brick Math works in many applications: for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and affordable. If you are a math teacher or a parent with a student at home who is learning K-8th grade math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves students' math test scores and hear what people who are using Brick Math have to say about the program.
 This is the time of year schools start planning for their summer programs. We’ve been busy lately, responding to school districts planning to use the Brick Math curriculum this summer.  Brick Math is the perfect way to engage struggling students in math summer school. Naturally, students enjoy using the bricks as math manipulatives. But even more importantly, Brick Math is a modular program that targets specific math skills. Students learn using different methods than other math programs, and experience shows that they respond very positively to the hands-on program.  Brick Math offers free curricula of summer programs for each of the 11 subject areas for schools who choose Brick Math as their summer school curriculum. These programs can be easily adapted to your school’s schedule. To view a sample of Brick Math’s summer program, click here. The sample shows Day 1 of a 12-day summer program for Basic Fractions.  The 11 Brick Math topics include: Brick Math has been shown to increase students’ test scores significantly. Students gain a real understanding of the reasons why behind the math when they learn with Brick Math.
Please call 802-751-8002 or email us if you'd like to learn more about how to use Brick Math in your school's summer program.  February's Lesson of the Month is on multiplying unit fractions by fractions. Unit fractions are those that have a 1 in the numerator. This lesson shows how to model the multiplication of any unit fraction by any other fraction. It's key to understanding what it actually means to multiply fractions together. The lesson is from Brick Math's Fraction Multiplication Using LEGO® Bricks. To get the February 2023 Brick Math Lesson of the Month, "Multiplying Unit Fractions by Fractions," plus a new lesson each month, click here. 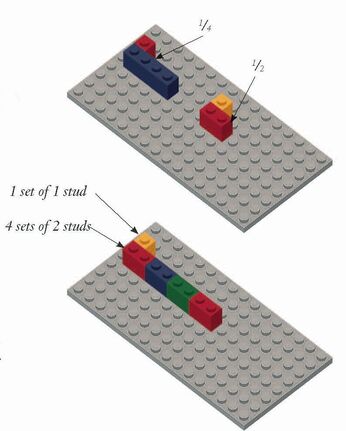 The lesson starts with a discussion of the term unit fraction, along with a discussion about how to determine which unit fraction is largest: 1/2, 1/3, or 1/4. The lesson then moves on to modeling two multiplication problems. Most 4th - 6th grade math teachers would agree that multiplying and dividing fractions is a very tricky subject for students to understand. The methods in Brick Math help make clear to students what is actually happening when two fractions are multiplied together -- not simply the process of multiplying the numerators and denominators together. This kind of deep understanding gives students a strong foundation in math that they can build on as they progress into middle school math and beyond. Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. This year, the program will expand to include grades 6 - 8, with the additional subjects Data and Statistics, Pre-Algebra, and Ratios and Proportions. Brick Math works in many applications: for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and affordable.
If you are a math teacher or a parent with a student at home who is learning K - 6th grade math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves students' math test scores and hear what people who are using Brick Math have to say about the program.  To celebrate "The Year of Brick Math," we're adding a new feature to the free Brick Math Lesson of the Month -- video! Dr. Shirley Disseler, author of the Brick Math curriculum, demonstrates the April 2021 lesson in a five-minute video that shows the concepts for comparing and ordering 3 fractions with unlike denominators. To get the April 2021 lesson, "Comparing and Ordering Fractions," and a link to the video lesson, plus a new lesson each month, sign up here. 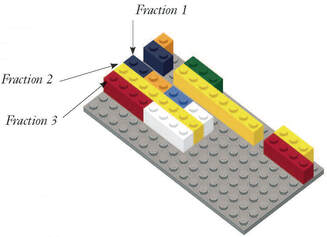 Elementary school math teachers know how tricky this skill can be for students to comprehend. When they look at the fractions 1/2, 3/8, and 3/4, many students will think that 3/8 is the biggest fraction of the three, since the denominator is the largest number. This lesson demonstrates the "fraction train" method of finding a common denominator using LEGO bricks to build the fraction models and model the equivalent fractions.  This lesson is from Chapter 7 of Basic Fractions Using LEGO Bricks in the Brick Math series. Students typically learn this skill in grades 3 - 4. Modeling the math with bricks makes it easy to learn. Try the free lesson with your students to see how much fun it is to learn with Brick Math! Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. It works well for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and are not shared between students. It adapts easily to online instruction.  If you teach math or have a student at home who is learning math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves student math test scores and hear what people who are using Brick Math have to say about the program. This lesson teaches students about the factors of 16. To get the March 2021 lesson, and a new lesson each month, sign up here. This might be my favorite lesson in the entire Brick Math curriculum, because it does so many things so well: 
 I use this lesson often when I’m demonstrating how well Brick Math works as a complete learning solution for elementary math. It always helps someone new to the program understand how effective the Brick Math methods are. Try the lesson with your student(s) today to demonstrate factors. The first two pages are from the Teacher Lesson Guide. The next two pages are for the student to use as they learn. There is a baseplate on the last page where the student can draw his/her final model of the factors of 16, plus space to list all the factors of 16. We guarantee they will have that “aha” moment when you teach factors this way!  Brick Math’s Basic Fractions Using LEGO® Bricks is a great way to get started with the topic of fractions. It starts by teaching the concept of fractions and progresses through unit fractions, addition and subtraction of fractions, and both like and unlike denominators. The use of LEGO® bricks to model the math makes it fun to learn, too! Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. It works well for homeschooling, math intervention, enrichment, and as a whole-school program. Materials are simple and are not shared between students. It adapts easily to online instruction. If you teach math or have a student at home who is learning math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves student math test scores and hear what people who are using Brick Math have to say about the program.  It’s been well established that fractions are tough for many students to learn. And it’s also clear that fractions are a very important building block for learning the higher-level math that follows, including decimals, ratios, and algebra. So we need a learning system that helps students achieve a deep understanding of fractions, not simply a regurgitation of some formulas or tricks. Luckily, Brick Math: Teaching Math Using LEGO Bricks includes techniques that really work when teaching students what fractions are all about. Here are four ways you can make it easier to learn fractions (all the illustrations and techniques here are from Brick Math's Basic Fractions Using LEGO Bricks–Teacher Edition):  bricks model (l to r): 4/8, 2/4, 1/2 bricks model (l to r): 4/8, 2/4, 1/2 1. Math is conceptual, so a student first needs to understand the idea of a fraction. The best way to learn that is by providing a visual presentation of a fraction. Brick Math, which teaches math using LEGO bricks as the modeling tool, is the perfect way to show what fractions are. A 1x1 brick next to a 1x2 brick clearly represents a fraction of 1/2. A LEGO brick with 2 studs next to a brick with 4 studs? Clearly showing 2/4. A four-stud brick next to an 8-stud brick models 4/8 without question. The studs on a brick are easy to count, even for young learners, and there is no mistaking the fraction that the bricks are showing. 2. Fractions refer to parts of a whole, but the whole must be defined clearly to understand the size of the fraction. The techniques used in Brick Math work well to clarify the concept of the whole. If the whole is 8, the brick that represents ½ of that whole has 4 studs. But if the whole is 6, the brick that represents ½ of that whole has 3 studs. LEGO bricks demonstrate this idea clearly.  factors of 8: 8, 4, 2, and 1 factors of 8: 8, 4, 2, and 1 3. Adding and subtracting fractions relies on students’ knowledge of multiplication. To find a common denominator, a student must have memorized multiplication tables to understand the idea of factors. That’s a hurdle many students have trouble with. But factors are easy to show with Brick Math. Students discover factors for themselves by manipulating the bricks. The illustration here shows all the factors of 8 in a way that students can immediately grasp (8, 4, 2, and 1).  9/12 (or 3/4) compared to 8/12 (or 2/3) 9/12 (or 3/4) compared to 8/12 (or 2/3) 4. It can be hard to understand how to put fractions in order. What’s bigger: 2/3 or ¾? That question becomes easy to answer using the Brick Math technique called the “fraction train.” That’s a way of modeling equivalent fractions with common denominators to visually demonstrate which fraction is larger. (Spoiler alert: ¾ is larger, because it is equivalent to 9/12, while 2/3 is equivalent to 8/12.)  There’s so much that’s hard about learning fractions. Brick Math makes the learning process easier so students can develop deep understanding of the math. That’s the key to future math success. Brick Math is a K-6 math curriculum that works for all students, whether they are in a classroom or learning at home one-on-one. If you have a student at home who is learning math, check brickmath.com. The website includes videos for both teacher/parent training and direct instruction of students. You can learn more about how Brick Math improves student math test scores and hear what people who are using Brick Math have to say about the program. If you are a teacher, check brickmath.com to learn how the curriculum can work in your classroom, whether it's in person, virtual, or hybrid. Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. It works well for math intervention, for enrichment, and as a whole-school program. Materials are simple and need not be shared between students. It adapts easily to online instruction. Contact us with any questions.  I recently had a customer tell me that her son didn’t understand the idea of factors until she tried Brick Math. When he saw the concept of factors made real with LEGO bricks, she said, he knew what they were! It’s exciting to hear when students finally “get it” because modeling with bricks makes all the difference for them. I started to think about that lesson on factors, and I realized it is the perfect way to demonstrate the power of Brick Math as a learning system. Here’s why Brick Math works so well to teach elementary math: it’s tactile (kids touch the bricks and build the models themselves), it’s visual (kids can see exactly what the numbers in a math problem represent), and it’s conceptual (kids understand the underlying idea behind the math when they discover it for themselves in a guided program). Let me show you how Brick Math works with that lesson on factors: This lesson models all the factors of 16 and demonstrates perfectly the meaning of “factor." Like all Brick Math lessons, it starts with some basic bricks and a baseplate to build on. Begin by placing one brick that has 16 studs on the baseplate (studs are the bumps on LEGO bricks). This can be a 2x8 brick or a 1x16 brick.The model shows 1 brick with 16 studs, so the multiplication fact shown is 1 x 16 = 16. 16 and 1 are factors of 16.  Next, take two bricks that each have 8 studs and place them next to the brick that’s already on the baseplate. It’s best if those two bricks are two different colors. You’ll use either two 2x4 bricks or two 1x8 bricks. Now the model shows 2 (bricks) x 8 (studs) = 16, and that 2 and 8 are also factors of 16. Now, here’s where the Brick Math program really becomes a powerful learning tool. For the next step, ask the student, “Are there 3 bricks that are all the same size that you can use to build the next row?” Let your students try with different bricks. They will demonstrate to themselves that there are none, so 3 can’t be a factor of 16. It’s so important that students discover for themselves while they are learning. That’s what helps them internalize what the math is all about. When they move on to looking for 4 bricks, they’ll find that four 2x2 bricks or 1x4 bricks do the trick. Now, they have 4 (bricks) x 4 (studs) = 16, so 4 is another factor of 16.  Have them look again for 5, 6, and 7 bricks that work in the model. They’ll quickly figure out that none of those numbers are factors of 16. They’ll move on to modeling eight 1x2 bricks, with the multiplication fact of 8 x 2 = 16. Finally, they can add sixteen 1x1 bricks to the model to complete all the factors with the multiplication fact of 16 x 1 = 16. When you look at the final model and count the number of bricks, the final model clearly shows the factors of 16: 1, 2, 4, 8, and 16. Dr. Shirley Disseler, developer of the Brick Math method, demonstrates this same lesson in the video below.  The concept of factors is key to learning multiplication, division, and fractions, so it’s in all three of the Brick Math books on those subjects: Multiplication, Division, and Basic Fractions. And it (almost) goes without saying: students have fun while they learn! If you teach math or have a student at home who is learning math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves student math test scores and hear what people who are using Brick Math have to say about the program.
Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. It works well for math intervention, for enrichment, and as a whole-school program. Materials are simple and need not be shared between students. It adapts easily to online instruction. Contact us with any questions.  Whether you're back to school in person or online, or some combination of the two, this free Brick Math Lesson of the Month is a great way to help students learn math. For September, it's a lesson from Fraction Multiplication Using LEGO® Bricks that shows how the commutative property works when multiplying fractions. Students typically learn about multiplying fractions in grades 4 - 6, but it is sometimes part of the curriculum when students are learning about fractions in grades 2 - 3. To get the free Lesson of the Month for September 2020, click here. Students should already understand that a x b = b x a (see Multiplication Using LEGO® Bricks, chapter 5). Now it's time for them to learn that the same commutative property holds when multiplying fractions. This lesson makes it clear to students by using bricks one way to model 1/2 x 6, and a different way to model 6 x 1/2. In both cases, the answer, 3, is the same. 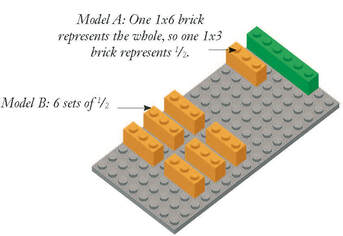 This lesson also shows how the two number sentences are used to describe different real-life situations: 1/2 x 6 means "one-half of six," while 6 x 1/2 means "six sets of one-half." So in real-life usage, 1/2 x 6 could describe "half of the six crayons in the box, or three crayons." And 6 x 1/2 could describe "six half-pizzas, or three whole pizzas." Using bricks to model these two scenarios really helps students understand the math.  Brick Math is a K-6 math curriculum that uses LEGO® bricks to model 11 different math subjects: Counting, Addition, Subtraction, Multiplication, Division, Basic Fractions, Basic Measurement, Fraction Multiplication, Fraction Division, Advanced Measurement and Geometry, and Decimals. It works well for math intervention, for enrichment, and as a whole-school program. Materials are simple and are not shared between students. It adapts easily to online instruction. If you teach math or have a student at home who is learning math, check brickmath.com. The website includes videos for both teacher training and direct instruction of students. You can learn more about how Brick Math improves student math test scores and hear what people who are using Brick Math have to say about the program. |
Categories
All
Archives
July 2024
|




